Análisis de Regresión: Descifrando las Relaciones entre Variables

El análisis de regresión es una técnica estadística poderosa que se utiliza para comprender y modelar las relaciones entre variables. Se emplea en una variedad de campos, desde la economía hasta la ciencia, y proporciona una herramienta fundamental para predecir resultados, identificar tendencias y tomar decisiones basadas en datos. En este artículo, exploraremos qué es el análisis de regresión, cómo funciona y cómo se aplica en el mundo real.

¿Qué es el Análisis de Regresión?

El análisis de regresión es un método estadístico que se utiliza para investigar y modelar la relación entre una variable dependiente (la que queremos predecir o explicar) y una o más variables independientes (las que utilizamos para hacer la predicción o la explicación). Esta técnica se basa en la idea de que las variables independientes pueden usarse para estimar o predecir los valores de la variable dependiente.

Cómo Funciona el Análisis de Regresión

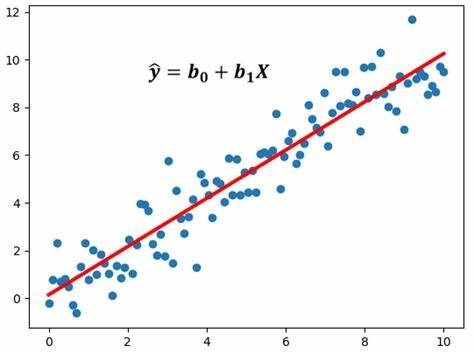
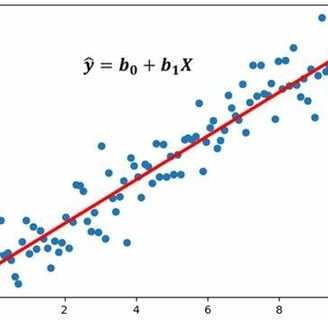
El análisis de regresión se basa en modelos matemáticos que intentan encontrar una ecuación que relacione las variables independientes con la variable dependiente. El tipo de análisis de regresión más común es la regresión lineal, que busca una línea recta que mejor se ajuste a los datos.

Existen dos tipos principales de análisis de regresión:

1. Regresión Simple: En la que hay una variable independiente que se utiliza para predecir la variable dependiente.

2. Regresión Múltiple: En la que hay múltiples variables independientes que se utilizan para predecir la variable dependiente. Este tipo es más común en situaciones del mundo real, donde los resultados pueden depender de múltiples factores.

Aplicaciones del Análisis de Regresión

El análisis de regresión tiene una amplia gama de aplicaciones en la vida real:

1. Economía: Se utiliza para predecir variables económicas como el crecimiento del PIB, la inflación o el desempleo basándose en múltiples factores económicos.

2. Ciencia: Se aplica en la investigación científica para modelar relaciones entre variables, como la relación entre la dosis de un medicamento y la respuesta en pacientes.

3. Mercadotecnia: Ayuda a las empresas a comprender la relación entre las inversiones en publicidad y las ventas, lo que les permite tomar decisiones informadas sobre su estrategia de marketing.

4. Ingeniería: Se utiliza en la ingeniería para predecir cómo las variables como la temperatura, la presión o la velocidad afectarán el rendimiento de un sistema.

La fórmula general para el análisis de regresión lineal simple es la siguiente:

Y=β0​+β01X+ϵ

Donde:

• Y es la variable dependiente que deseas predecir.

• β0​ es la ordenada al origen (el valor de Y cuando X es igual a cero).

• β1​ es la pendiente de la regresión (representa cuánto cambia Y por cada unidad de cambio en X).

• X es la variable independiente que se utiliza para predecir Y.

• ϵ representa el error o el residuo, que es la diferencia entre el valor real de Y y el valor predicho por el modelo.

El objetivo del análisis de regresión es estimar los valores de β0​ y β1​ que mejor se ajusten a los datos, de manera que el modelo pueda predecir con precisión los valores de Y en función de X.

Para el análisis de regresión múltiple, donde hay múltiples variables independientes, la fórmula se extiende de la siguiente manera:

Y=β0​+β1X1+β2X2+…+βp+Xp​+ϵ

Donde:

• X1​,X2​,…,Xp​ son las variables independientes adicionales.

• β1​,β2​,…,βp​ son los coeficientes que se estiman para cada variable independiente.

El análisis de regresión busca estimar los valores de β0​,β1​,β2​,…,βp​ que mejor ajusten el modelo a los datos observados, de modo que se pueda realizar una predicción precisa de Y en función de X1​,X2​,…,Xp​.

Pasos en un Análisis de Regresión

Un análisis de regresión típico implica los siguientes pasos:

1. Recopilación de Datos: Reúne datos sobre las variables relevantes.

2. Selección del Modelo: Elige el tipo de regresión adecuado para tus datos (simple o múltiple).

3. Análisis Exploratorio de Datos: Examina los datos para identificar tendencias, valores atípicos y relaciones preliminares.

4. Ajuste del Modelo: Utiliza software estadístico para ajustar el modelo de regresión a los datos.

5. Evaluación del Modelo: Evalúa la calidad del ajuste y la significación de las variables independientes.

6. Predicciones y Conclusiones: Utiliza el modelo para hacer predicciones y llegar a conclusiones basadas en los resultados del análisis.

Conclusión

El análisis de regresión es una herramienta estadística fundamental que permite entender y modelar las relaciones entre variables en una amplia variedad de campos. Desde la economía hasta la ciencia y la mercadotecnia, el análisis de regresión ayuda a tomar decisiones basadas en datos y a predecir resultados. Si bien puede ser una técnica compleja, su capacidad para proporcionar información valiosa lo convierte en una habilidad valiosa para cualquier persona que trabaje con datos en un contexto analítico.